Мерзляк Геометрія 7 клас відповіді
Вправа 568
Умова:
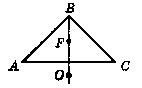
Точки F i О - центри вписаного й описаного кіл рівнобедреного трикутника ABC відповідно (рис. 311). Вони розташовані на однаковій відстані від його основи АС. Знайдіть кути трикутника ABC.
Відповідь:
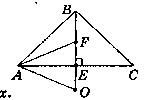
Дано:
∆АВС - рівнобедрений, АВ = ВС.
F - центр вписаного кола, О - центр описаного кола. ОЕ = EF.
Знайти: кути ∆АВС.
Розв'язання:
F - центр вписаного кола. Отже, AF - бісектриса ∟BAC.
Нехай ∟EAF = ∟FAB = х, тоді ∟BAE = 2х.
Розглянемо ∆AFE - прямокутний (∟E = 90°).
За властивістю гострих кутів маємо: ∟EFA = 90° - х.
Розглянемо ∆АЕВ - прямокутний (∟E = 90°), ∟ABE = 90° - 2х.
За умовою О - центр описаного кола, тобто ОА = ОВ - радіуси описаного кола.
Розглянемо ∆ОАВ - рівнобедрений (ОА = ОВ).
За властивістю кутів рівнобедреного трикутника маємо: ∟ABO = ∟BAO.
Розглянемо ∆АЕВ - прямокутний (∟E = 90°).
∟ABE = 90° - 2х; ∟ABO = ∟BAO = 90° - 2х.
∟OAE = ∟OAB - ∟EAB; ∟OAE = 90° - 2х - 2х = 90° - 4х.
За умовою ОЕ = EF i AE ┴ OF. Отже, АЕ - медіана i висота.
Звідси маемо: ∆ОАF - рівнобедрений. ∟OAF = 2∟OAE = 180° - 8х.
За теоремою про суму кутів трикутника маємо:
∟OAF + ∟AFO + ∟FOA = 180°.
180° - 8x + 90° - x + 90° - x = 180°; 180° - 10х = 0; 10х = 180°; x = 18.
∟BAC = ∟BCA = 18° • 2 = 36°;
∟ABC = 180° - 2 • 36° = 180° - 72° = 108°.
Biдповідь: 36°, 36°, 108°.
Повідомити про помилку
Обгрунтуй, що саме не так!




