Математика 6 клас
Вправа 760
Умова:
Задача Гіппократа1. Доведіть, що на рисунку 50 сума площ зафарбованих фігур («серпиків») дорівнює площі прямокутника.
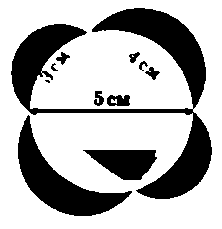
Відповідь:
Площа прямокутника: Sпр = 3 см • 4 см = 12 см2.
Площа білого круга з діаметром 5 cм: Sкр = 25∏/4 см2.
Площа білих серпиків: Sбіл.серп. = Sкр - Sпр = (25∏/4 - 12) см2.
Площа чотирьох зафарбованих півкругів: Sзаф. = (9∏/4 + 16∏/4) см2 = 25∏/4 см2.
Отже, площа серпиків: Sсерп = Sзаф - Sбіл.серп. = 25∏/4 см2 - (25∏/4 - 12) см2 = 12 см2.
Таким чином, Sсерп = Sпр.
Правила до параграфу "Довжина кола. Площа круга"
Повідомити про помилку
Обгрунтуй, що саме не так!




