Геометрія 7 клас
Вправа 322
Умова:
Промінь ОС розбиває кут АОВ на два кути так, що ∟AOC : ∟BOC = 3 : 5. Знайдіть кут між променем ОС i бісектрисою кута, суміжного з кутом АОВ, якщо кут ВОС на 42° більший за кут АОС.
Відповідь:
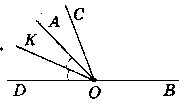
Нехай ∟AOB - даний, ∟AOC : ZBOC = 3 : 5.
∟DOA i ∟AOB - cyміжні, OK - бісектриса ∟DOA, ∟BOC більше ∟AOC на 42°.
Знайдемо ∟KOC.
Нехай х - одна частина, тоді ∟AOC = 3х, ∟BOC = 5х. Так як ∟BOC
більше ніж ∟AOC на 42°, то 5х - 3х = 42; 2х = 42; х = 21.
∟AOC = 3 • 21° = 63°, ∟BOC = 5 • 21° = 105°.
∟AOВ = ∟AOC + ∟BOC, ∟AOB = 63° + 105° = 168°.
∟AOB + ∟DOA = 180° (як суміжні).
∟DOA = 180° - 168°, ∟DOA = 12°.
∟DOK = ∟КОА = 1/2∟DOA = 12°: 2 = 6° (OK і бісектриса ∟DOA).
∟КОС = ∟KOA + ∟AOC, ∟КОС = 6° + 63° = 69°.
Biдповідь: ∟КОС = 69°.
Повідомити про помилку
Обгрунтуй, що саме не так!




