Мерзляк Геометрія 7 клас

Вправа 371

 

Умова:

Бісектриси АК i СМ трикутника ABC перетинаються в точці О, ∟BAC = 116°, ∟BCA = 34°. Знайдіть кут АОС.

 

Відповідь:

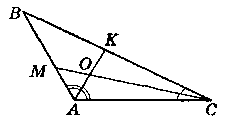
Нехай дано ∆АВС, ∟BAC = 116°, ∟BCA = 34°, АК i CM - бісектриси.
Знайдемо ∟AOC.
∟BCM = ∟MCA = 1/2∟BCA = 34° : 2 = 17° (CM - бісектриса).
∟BAK = ∟KAC = 1/2∟BAC = 116° : 2 = 58° (АК - бісектриса).
Розглянемо ∆АОС:
∟OAC + ∟AOC + ∟OCA = 180°.
∟AOC = 180° - (17° + 58°) = 180° - 75° = 105°.
Biдповідь: ∟AOC = 105°.