Геометрія 7 клас решебник відповіді гдз

Вправа 434

 

Умова:

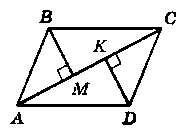
На рисунку 264 АВ = CD, АВ ‖ CD, BM ┴ AC, DK ┴ АС. Доведіть, що BM = DK.

 

Відповідь:

Дано:
AB = CD; AB ‖ CD; BM ┴ AC; DK ┴ AC.
Довести: BM = DK.
Доведения:
За умовою AB ‖ CD, AC - січна.
За ознакою паралельності прямих маємо: ∟ВАС = ∟DCA (внутрішні різносторонні).
За умовою ВМ ┴ АС, тоді ∟BMA = 90°; DK ┴ АС, тоді ∟CKD = 90°.
Розглянемо ∆ВМА i ∆CKD:
1) ∟BMA = ∟CKD = 90°;
2) ∟ВАМ = ∟DCK;
3) AB = CD (за умовою).
За ознакою piвностi прямокутних трикутників маємо: ∆ВМА = ∆DKC.
Звідси BM = DK (як piвнi елементи рівних фігyp).
Доведено.