Геометрія 7 клас гдз

Вправа 437

 

Умова:

На сторонах кута з вершиною в точці В позначили точки A i С так, що AВ = ВС. Через точки А і С провели прямі, які перпендикулярнi до сторін ВА i ВС відповідно та перетинаються в точці О. Доведіть, що промінь ВО - бісектриса кута ABC.

 

Відповідь:

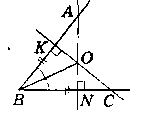
Дано:
∟B; AB = ВС; СК ┴ KB; AN ┴ NB; AN ∩ CK = 0.
Довести: BO - бісектриса ∟ABC.
Доведения:
За умовою СК ┴ KB, ∟CKB = 90° i AN ┴ NB, тоді ∟ANB = 90°.
Розглянемо ∆ANB i ∆CKB:
1) ∟ANB = ∟CKB = 90°;
2) AB = ВС (за умовою);
3) ∟В - спільний.
За ознакою piвностi прямокутних трикутників маємо ∆ANB = ∆СКВ.
Звідси ∟BAN = ∟BCK (як piвнi елементи piвниx фігyp);
BN = ВК. Якщо АВ = ВС i BN = ВК, тоді АК = NC.
Розглянемо ∆АОК i ∆СОN:
1) ∟OКA = ∟ONC = 90°;
2) АК = NC;
3) ∟АOК = ∟NOC (вертикальні).
За ознакою piвностi прямокутних трикутників маємо: ∆АОК = ∆CON.
Звідси OK = ON.
Розглянемо ∆ONB i ∆OKB:
1) ∟OKB = ∟ONB = 90°;
2) ОВ - спільна сторона;
3) OK = ON.
За ознакою piвностi прямокутних трикутників маємо: ∆ONB = ∆ОКВ.
Тоді ∟OBN = ∟OBK. Тоді ОВ - бісектриса ∟ABC.
Доведено.